Тренирайте ума си с ребуси и загадки
Още от древността математиката е неразделна част от нашето ежедневие. Нашето разбиране за математиката и постоянното желание да разширим обхвата на знанията си за света ни отведоха далеч, така че днес светът, какъвто го познаваме, не би бил възможен без математиката.
Математиката е език на материята и допринася за всички наши методични и систематични поведения. Математиката помогна да въведем ред в обществото и да предотвратим хаоса и катастрофите. Много от нашите наследени човешки качества се развиват от математическите теории, като нашето пространствено съзнание, нашите умения за решаване на проблеми, способност да разсъждаваме, креативност и комуникация.
Нещата, които не бихте очаквали да имат някаква връзка с математиката, всъщност се свеждат до основна нужда от математика и структурата, която тя внася в ежедневието ни.
Освен това математиката присъства във всеки занаят или професия - независимо дали сте художник или учен.
Художникът ще използва своята креативност, ще планира и изчислява с всяко движение на четката дължината и въздействието на отпечатъка, който поставя върху платното.
Добавете към това факта, че те ще имат нужда да заделят бюджет за неща като консумативи, инструменти, ателиета и т.н. и ще се наложи да посмятат, за да определят подходящи цени за своите произведения.
Учените ще бъдат в пряк контакт с числа, измервания, уравнения и формули в ежедневните си задачи и математиката ще властва над всички изследвания, които правят.
Всичко това звучи дълбоко и плашещо, нали? Да кажете, че математиката управлява почти всичко на този свят и че нейното значение за живота е неизмеримо? Не се притеснявайте, тук идва забавната част!
Превръщане на математическите задачи в ползи
Математиката има репутацията на скучен предмет. Но това не е така! Нещо повече, чрез въвеждане на забавни елементи - логически задачи и математически пъзели - в преподаването на математически теории и концепции, много повече ученици ще бъдат отлични в тази област! Толкова е лесно просто да изключим и да пропуснем да приемем каквато и да е информация, когато просто не сме толкова заинтересовани. Но начинът да запазите и обработите тази важна информация и да не я оставите просто да изчезне е да се наслаждавате на работата по нещата.
Знаете ли, че можете да се забавлявате много, докато учите математика и множеството трикове и пъзели, които тя представя? Повечето от нас не могат да устоят на добра гатанка и решаването на трудни логически пъзели е фантастична главоблъсканица. Да направите понятия като алгебра, дроби и вероятности по-забавни не е толкова трудно, колкото звучи! Ако не ни вярвате, опитайте тези математически пъзели!
Точно така, възможно е да практикувате математика, докато се забавлявате! Независимо дали става дума за оптична илюзия, картинен пъзел или логически игри, измислянето на отговора на сложен пъзел е чудесен начин да подобрите уменията си за решаване на проблеми.


Тествайте Ума Си с Математически Пъзели
В стремежа си да разбере света около себе си, човекът е използвал математика в опит да намери осезаеми доказателства. Историята на математиката е изпъстрена от велики умове, борещи се с великите енигми на своето време.
Математическите пъзели и главоблъсканици комбинират математически формули и разсъждения с числа, изчисления и числа. За решаването на такива пъзели не е необходимо човек да притежава мозъка на математически гений, но е важно да възприеме логичен подход и да приложи математическите умения, които е научил - от просто умножение и деление до квадратни уравнения. Така че се пригответе да тествате вътрешния си математик с тези 5 предизвикателни пъзела, които може да срещнете в часовете по математика. Но първо! Нека помислим как и защо тези главоблъсканици са толкова полезни за нас.
Ползите от математическите главоблъсканици
Не всичко е в главата ти! Мозъчната тренировка е еднакво полезна за цялото ви тяло и благополучие. Поддържането на ума активен може да има различни ползи, включително намален риск от деменция. Като цяло би трябва да поддържате ума, както и тялото активни. Има различни неща, които поддържането на ума ви активен с когнитивно обучение може да направи за вас, като например:
- Подобрете способността си да запомняте
- Намалете риска от психични заболявания като деменция
- Подобрете скоростта си на мислене
- Предотвратете скуката
- Подобрете концентрацията
Също така, обмисляли ли сте някога факта, че всичко променя мозъка ви? Всеки нов човек, който срещате, всяка нова история, която четете, всяко ново цвете, което помирисвате... има толкова много „първи“, които продължават да се случват през целия ни живот, че вероятно дори не се замисляме. Въпреки това, когато седнете и мислите за това, мозъкът ви непрекъснато се развива и се влияе от околната среда.
Така че, ако все още се съмнявате как малко тренировка на мозъка може да ви помогне, тогава просто помислете за това: ако, подобно на много други, едно-единствено изображение на знаменитост, изглеждащо според вашата представа за съвършенство, може да предизвика силно чувство на бизнес мотивация да отидете на фитнес, да си купите нови дрехи, да смените прическата - тогава не може ли една малка математическа игра да промени начина ви на мислене?
Кой знае какво може да постигне редовното обучение на мозъка откъм това как подхождате към математиката и как мислите за нещата като цяло! Ето една "формула", която може да ви хареса и която може да се приложи за вас, ако учите математика. Математика = Контрол = Самоусъвършенстване = Удовлетворение
Мозъчни въпроси: Проблемът със 100-те затворници
В един затвор има 100 затворници, осъдени на смърт. Изневиделица директорът на затвора предлага предизвикателство. Той дава на всеки затворник номер между 1 и 100, след което инсталира в кабинета си шкаф със 100 чекмеджета, всяко от които съдържа произволно число между 1 и 100, съответстващо на тези, присвоени на затворниците. Всяко число се появява само веднъж. Той моли всеки затворник да отвори 50 чекмеджета и да провери броя във всяко. След като всеки затворник влезе в кабинета, му е забранено да общува с останалите затворници, нито да променя последователността на тегленията или да оставя каквито и да е улики. Никой затворник няма да знае какви числа са видели другите затворници. Директорът на затвора дава два възможни резултата:
- Всички затворници намират съответните си номера и всички са помилвани.
- Никой не намира номерата си и всички са екзекутирани.
Какъв е шансът всеки затворник да намери чекмеджето, отговарящо на неговия номер? Според закона за математическата вероятност шансът всички да бъдат помилвани е ( 1/2 ) 100.
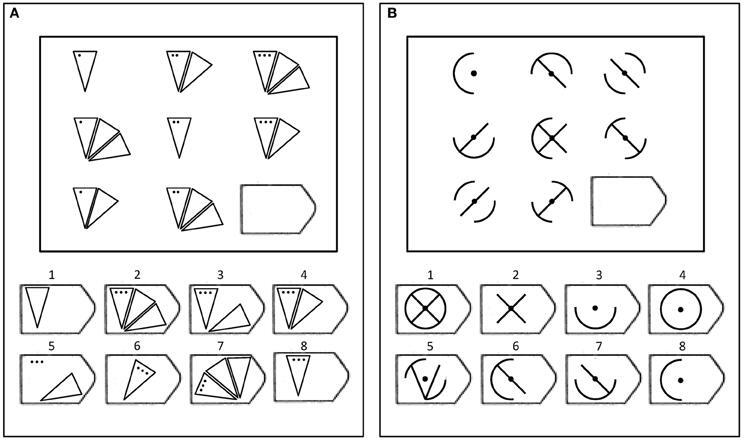
3-те бога
Зад три знака, наречени A, B и C, се крият 3 бога, известни като „истински“, „фалшив“ и „случаен“ . „Истинският“ бог винаги отговаря с истината, „фалшивият“ бог винаги лъже, а „случайният“ се редува непредсказуемо между двамата. Предизвикателството е „просто“!: Открийте съответните идентичности на A, B и C, като зададете само три въпроса, чийто отговор е верен или неверен. Всеки въпрос може да бъде зададен само на един бог, но ако решите да разпитате един бог повече от веднъж (максимум три пъти), другите богове няма да могат да отговорят. Вашите въпроси може да не са свързани един с друг.
Триъгълната торта
Когато подготвя класа си за състезание по математика, учител решава да предложи на учениците си торта под формата на триъгълник с три неравни страни. Той прави поръчка в сладкарница, като дава размерите на трите страни на тортата. Сладкарят поръчва кутия за тортата, като дава същите размери. Когато тортата е готова обаче, той установява, че въпреки че измерванията са спазени, формата е по-скоро симетрична, отколкото идентична с тази на тортата. Обажда се на учителя по математика, за да го пита как да нареже тортата така, че да влезе в кутията. Учителят отговаря, че две съкращения ще са достатъчни. Как трябва да бъдат направени?
Проблемът с котката и мишката
Котка и мишка решават да играят на "глави или опашки". За да оживят играта, те решават да променят правилата: Всеки играч трябва да избере комбинация от 3 резултата (напр. глави, опашки, глави). Те хвърлят монетата много пъти и първият, който види една от неговите комбинации да се появява в три последователни хвърляния на монети, печели играта. Двамата играчи не могат да избират една и съща комбинация. Котката, чувствайки се като по-силен играч, започва първа. Мишката, по-умната от двете, решава да го пусне напред. Как може да се увеличи шансът за печалба за всеки играч?
Патицата и котката
В средата на кръгло езерце има патица. На ръба на това езерце стои нетърпелива котка. Докато патицата би искала да опита тревата на ръба на езерцето, котката много би искала да опита патицата! Котката не знае как да плува и се страхува твърде много от водата, за да влезе в езерото. Междувременно патицата има крила, които са твърде малки, за да позволят да отлети. Знаейки, че котката може да бяга четири пъти по-бързо, отколкото патицата може да плува, възможно ли е патицата да стигне до ръба на езерото, без да бъде хваната от котката?
Още математически главоблъсканици, за да предизвикате своите математически способности
Мозъчна закачка е въпрос, чийто отговор трябва да бъде забавен. Разбира се, не всеки харесва главоблъсканици – в този случай те биха били по-скоро разочароващи, отколкото забавни, но щом ги овладеете, вие също ще ги намерите за забавни.
Има всички видове главоблъсканици; някои включват условия или ситуации; други се основават на определена последователност. Например:
Бащата на Мери има пет дъщери: Нана, Нене, Нини и Ноно. Как се казва петата дъщеря?
Някои може да последват модела на гласните и да провъзгласят Нуну за петата дъщеря, но както често се случва в главоблъсканиците, отговорът е във въпроса.
Ако бащата на Мери има пет дъщери, тогава Мери трябва да е една от тях... нали?
Математическите закачки също могат да имат толкова очевидни отговори, но понякога изискват повече мисъл. Например:
Ако три птици снасят три яйца за три дни, колко яйца снася една птица за един ден?
Отговорът на това е двусмислен. От математическа гледна точка една птица снася 1/3 от яйце за един ден. Въпреки това, тъй като никоя позната на човека птица не може да снесе само една трета от яйце, логичният отговор е или едно , или нито едно.
Вижте какво имаме предвид под разочароващо?

Мозъчните закачки трябва да са подходящи за ниво; естествено, не бихме искали да измъчваме ученици по математика с пъзели, които изискват познания за по-високи алгебрични функции, когато те не са на този етап на учене!
Мозъчни закачки за по-малки учащи
Изисква се малко добавяне: използвайки само 8 осмици, как можете да ги съберете заедно, за да се равняват на 1000?
Отговор: 888+88+8+8+8 = 1000
Мисля за трицифрено число. Втората цифра е четири пъти по-голяма от третата, а първата е с три по-малка от втората.
Отговор: 141
Кои три числа дават един и същ резултат, независимо дали се добавят или умножават заедно?
Отговор: 1, 2 и 3
Лиъм направи четири снежни топки в понеделник. Във вторник той направи девет, а в сряда 14. Колко направи в четвъртък и петък?
Отговор: увеличавайте количеството с пет всеки ден.
По-напреднали мозъчни закачки
Най-високата температура, регистрирана на Хийтроу на 1 януари, беше -1 градус. На 2 януари беше 4 градуса. Каква е била температурата на 3 януари, ако средната температура за първите три дни на януари е била 2 градуса?
Отговор: 3 градуса
Продавач на хот-дог иска да купи равни количества колбаси и кифлички, но кифличките се доставят в опаковки по 10, а колбасите в опаковки по 8. Колко опаковки от всяка ще трябва да купи продавачът, за да постигне целта си?
Отговор: 10 пакета колбаси и осем пакета кифли.
Всички тези твърдения са верни: AxB=12; A+B+C=12; и BA=1. Какви последователни числа са представени от A, B и C?
Отговор: A=3, B=4, C=5
Разликата между мозъчни закачки и гатанки
Много хора не правят разлика между тези два типа игри. В крайна сметка и двата въпроса са предназначени да ви накарат да се замислите ... нали?
Разликата между главоблъсканиците и гатанки се крие в тяхното намерение.
Гатанката понякога използва двойни значения или други фрази, които изискват изобретателност и нелинейно мислене за решаване. Ето един отличен пример за това:
Какво започва с Т, завършва с Т и има Т в себе си? Чайник!
Мозъчната закачка, от друга страна, обикновено не използва сложна конструкция или множество значения:
Аз съм нечетно число. Махнете една буква и ставам квит. Кое число съм аз?
Отговорът, седем, е два пъти верен: 7-1=6, което е четно число , добавено към факта, че премахването на S оставя думата четна!
Мозъчните закачки обикновено са за забавление, така че биха били ефективни като загрявка или разбиване на лед в началото на урока по математика.
Ако сте преподавател, може да запазите запас от тези главоблъсканици в резерв, за да разведрите настроението и да подготвите своя обучаван психически да учи.
Грижачи: вие също можете да култивирате мисленето на вашите подопечни, като пускате от време на време главоблъсканица.
В задръстване? Чакате в кабинета на лекаря? Идеалното време за тренировка на ума!

Математически логически пъзели
Точно като традиционните пъзели, чиито преплетени части образуват цялостна картина, логическите пъзели възприемат същия принцип – без частите.
Логическите пъзели изискват от участника да сглоби правилно тези фигуративни части, като използва само своите мисловни процеси... и може би молив, за да си прави бележки.
Някои от по- популярните логически пъзели, включващи числа, включват Sudoku и KenKen. Един специфичен логически пъзел, който помете света и дори беше централна тема на холивудския блокбастър „Преследването на щастието“, е...
Можете ли да съберете парчетата, за да излезете с правилния отговор?

Кубът на Рубик , плод на въображението на архитекта Ерно Рубик, плени света веднага след премиерата си през 1980 г. Оттогава няколко повторения се развиха от първоначалната кубоидна концепция: Змията на Рубик и Магията на Рубик, както и множество специално изработени пъзели и дори цифрови версии.
Днес, почти 40 години след дебюта на куба, страни по целия свят са домакини на състезания по скоростно кубче. Някои от предизвикателствата включват сляпо кубиране, кубиране с крака и, разбира се, решаване на пъзели с кубчета за най-кратко време. Световната кубинг асоциация регулира и спонсорира тези събития.
Рубик измисля пъзела с кубчета като предизвикателство за своите студенти – по това време той беше професор по архитектура.
Устройството, направено от дърво и държано заедно с гумени ленти, има за цел да даде на неговите ученици практически опит да манипулират триизмерен обект.
Той не възнамеряваше да създаде логически пъзел и наистина не знаеше, че е такъв, докато не се опита да го върне до първоначалното му състояние – всички цветове от съответните им страни.
Така че, ако се окажете в бездействие и ръцете ви просто треперят за нещо, вземете кубчето на Рубик и вижте дали можете да измислите нов алгоритъм за решаването му!
Междувременно ето няколко други логически пъзела, в които да опитате ръката си. За съжаление, те не са от вида, който можете да манипулирате физически!
Имате торба, съдържаща 10 ябълки. Срещате 10 приятели, всеки от които иска ябълка. Разпределяте ябълките – по една на всеки приятел и остава една в торбата. Как е възможно това?
Отговор: вие сте дали на последния приятел торбата с последната ябълка.
Имате три торбички, всяка от които съдържа две топчета. Чанта 1 има две сини топчета, торба 2 има две зелени топчета, а торба 3 има една зелена и една синя топка. Посягайки в една торба, изваждате син мрамор; колко вероятно е мраморът, останал в тази торба, да е син?
Отговор: има 2/3 вероятност останалият мрамор също да стане син.
Как можете да съберете две 3-цифрени числа, така че винаги да е равно на 1089?
Отговор: изберете 3-цифрено число и след това го обърнете. Извадете първоначалното си число от обърнатото число и обърнете този резултат. Добавете това число към резултата от изваждането, за да получите 1089
4-инчов масивен куб от дърво е боядисан в червено от всичките 6 страни. След това се нарязва на 1-инчови кубчета. Колко от тези кубчета ще имат 3 червени страни, колко ще имат 2 червени страни или 1 червена страна и колко изобщо няма да имат червено?
Отговор: 8 кубчета ще имат 3 червени страни, 24 ще имат 2 червени страни, 24 ще имат 1 червена страна и 8 няма да имат никакво червено.
Някои от тези пъзели изглежда противоречат на логиката, както в случая с #2: как може да има 2/3 вероятност второто топче да е синьо, ако зелените топчета са повече от сините след първото теглене?
Този феномен е известен като проблемът на Монте Хол и разчита на интуицията и елиминирането.
1. Можете да премахнете чантата , съдържаща само зелени топчета; явно не си избрал от него. Остават 2 торбички, всяка от които съдържа син мрамор.
2. След като (фигуративно) сте елиминирали 2 зелени топчета, броят на сините топчета, които все още са в торбите, е двойно по-голям от броя на зелените топчета...
3. Тъй като общият брой топчета, от които да избирате, е 3 и две от тях са сини, имате шанс 2 в 3 отново да изберете синьо.
Повечето твърдят, че ще имате 50% шанс да изберете отново синьо, но сега, след като направихме изчисленията, виждаме, че това предположение не е правилно!
По същия начин с боядисаното в червено кубче. Мнозина изглежда приемат, че кубът е кух и пренебрегват добавянето на осемте небоядисани куба, които съставляват сърцевината на по-големия куб.
И накрая, торбата с ябълки и всички тези алчни приятели: мнозина усещат, че всяка ябълка ще бъде извадена от торбата, за да бъде раздадена, но това е необходимо само за първите девет ябълки.
Нека десетият алчен приятел изхвърли торбата с ябълки вместо вас!
Що се отнася до трите цифри, които винаги са общо 1089? Всъщност е доста интересно да видим колко забавна може да бъде играта с алгебра.
Човекът и мистерията
Човекът винаги се е стремял да разбере света, в който е еволюирал. Той е изследвал неуморно, консултирал се е с безброй томове и е обсъждал със своите съвременници, за да разбере по-добре света на математиката. Всеки отговор води до още въпроси.
Желанието да решаваме загадки е част от нашето генетично наследство: Ние сме родени да търсим отговори .
Защо сме тук, на Земята? Има ли живот след смъртта? Кои са били първите хора? Как са живели? От древността някои от големите мистерии, вкоренени в математиката и физиката, са убягвали на нашето разбиране:
- Как са построени пирамидите в Египет; с каква цел са били така подредени?
- Как можем да обясним математическия гений на велики личности като Леонардо да Винчи, Архимед, Нютон, Анри Поанкаре и Стивън Хокинг?
- Други археологически мистерии от математическо значение, които все още объркват нашето разбиране, включват: Сфинксът в Египет, колоната на Делхи; железен стълб с височина повече от 7 метра и на 1600 години, който никога не е ръждясвал, и Мегалитните сфери на Коста Рика; 300 сфери с диаметър 2 метра и тегло 16 тона, чийто произход и предназначение остават неизвестни.

Поглъщането в математически задачи може да бъде много добър начин някой да забрави проблемите си.
За да направите това, може да се наложи да използвате:
- геометрия
- ментална аритметика
- приложна математика
- дълго деление
- математически теореми
- тригонометрия
Математически пъзели и уроци
Да обичаш математиката... или не
Всички ли трябва да обичаме математиката и математическите уравнения? Защо те имат значение? Защо някои хора се самоизключват, когато става въпрос за тази тема?
Какви са причините да обичате да решавате задачи по математика?
- Помощта по математика може да установи дали нещо е вярно или невярно.
- Има известна елегантност в математическите теории. Важното е винаги да се стремите да разбирате , вместо да учите десетки формули и теореми, без да схващате техните тънкости.
- Математиката може да бъде много полезна в покера, когато става въпрос за спечелване на залог!
- Математиката е много мощен инструмент: възможно е да постигнем изключителни резултати и приложения, които на пръв поглед изглеждат извън нашия обсег.
- Благодарение на математиката вие не само ще придобиете по-задълбочено разбиране за света около вас, но ще можете да се доближите до други дисциплини като физика, химия и икономика.
- Математиката е като игра, тъй като е логична, формална и стимулира мозъка ви, както правят игри като шах, судоку и дори Candy Crush Saga!
- След като сте схванали основните принципи, математиката става нещо като втора природа, която ви помага да разбирате и решавате проблемите около вас.
Защо мнозина намират математиката за толкова трудна?
- Математиката е език и за да я използвате добре, трябва да овладеете нейната правила - такива, които трябва да се научат и такива, които да се прилагат без съмнение.
- Като предмет изисква голяма доза самодисциплина. Не е достатъчно да се задоволявате с „почти“ по математика: трябва да сте методични.
- И накрая, математиката е взискателна дисциплина, която изисква редовна и последователна практика. Независимо дали сте сами пред екрана или взимате частни уроци, трябва да сте трудолюбиви и постоянни, включително извън часовете по математика, ако сте в такава програма за обучение.
Математически способности
Основните теми, които ще срещнете в учебните часове по математика са:
- Числа
- Алгебра
- Съотношение, пропорция и скорости на изменение
- Геометрия и мерки
- Вероятност
- Статистика
Със сигурност има място за забавление сред тези модули? Разбира се, голяма част от това зависи от вашия учител, неговия стил на преподаване и времето, с което разполагате, за да покриете съдържанието в уроците. Въпреки това, няма нищо лошо да попитате дали вашият учител е чувал за тези математически игри и дали бихте могли да опитате подобни пъзели и игри по време на час! Учениците следва да:
- Разбиране на математиката и математическите процеси по начин, който насърчава увереността, удоволствието, и осигурява здрава основа за напредък.
- Разширен обхват от математически стандарти и практики
- Разбиране на кохерентността и прогресията в математиката и как са свързани различните нейни области.
- Прилагане на математиката в други области на обучение и разбиране за широкото приложение на математиката в обществото.
- Използване на математически знания, за да се взимат логични и обосновани решения при справянето с проблеми - както в рамките на чистата математика, така и в живота.
- Разсъждава се логично и се разпознават неправилни разсъждения.
- Конструиране на математически доказателства.
- Решаване на предизвикателни проблеми, изискващи стратегическо мислене.
- Разпознаване кога математиката може да се използва за анализиране и решаване на проблем в контекст.
- Представяне на ситуациите математически и разбират връзката между проблемите в контекста и математическите модели, които могат да бъдат приложени за решаването им.
- Чертаене на диаграми и скициране на графики за изследване на математически ситуации и интерпретиране на решения.
- Вадене на изводи и заключения, когато се използват математически разсъждения.
- Тълкуване на решения ефективно в контекста на проблема.
- Четене и разбиране на математически аргументи, включително обосновки на методи и формули.
- Четене и разбиране на статии относно приложенията на математиката.
- Ефективно използване на технологии като калкулатори и компютри.
- Поемане на отговорност за обучението и собствена оценка на математическото себеразвитие.
Математика на университетско ниво
На това ниво можете да изберете да учите за академична степен по математика, но също така можете да изберете да се съсредоточите върху специалност като математически финанси, математическа физика, математическа биология, актюерска математика, история на математиката, теория на относителността, квантова теория или медицинска статистика. Много от тях ще са достъпни като модули в следващите години.
Разбира се, дори ако харесвате математиката и смятате, че сте доста добър в нея (особено след всичките тези игри с мозъчни закачки!), тогава не е нужно да учите математика, да речем. Защо не разгледате идеи като икономика, инженерство, компютърни науки, физика или теоретична физика; или друг научен предмет като химия, биология или психология, или счетоводство и финанси?
Къде може да ви отведе математиката професионално?
Ако търсите кариера в областта на финансите, тогава се изисква известно ниво на математическа квалификация, но може да не е задължително да имате нужда от диплома. Области, които бихте могли да обмислите, са счетоводство, актюерска работа, управление на инвестиции, инвестиционно банкиране и банкиране на дребно. Освен финансовия сектор, има индустрии като инженерство и информационни технологии, които могат да се възползват от някой, който е добър с числата.
Като алтернатива, различни пътища, които следват завършилите математика, включват роли като офицер от отбраната и разузнаването, статистик, оперативен изследовател, академичен математик, учител по математика в основно или средно училище или позиции в закона, медиите, бизнеса или публичния сектор. Можете да видите какви работни места има за любителите на математиката, като посетите уебсайт за работа.
Надяваме се, че вече сте се убедили, че уроците по математика разпалват невроните ви и могат да ви отведат на много места! Също толкова важно, те ни осигуряват по-добро разбиране на нашия свят. И накрая, когато знаете къде да търсите, е лесно да видите отпечатъка на математиката в нашето ежедневие!
Обобщи с помощта на AI















