Това, което знаем, е капка, а това, което не знаем, е океан.
Исак Нютон
В необятната математическа вселена формулите заемат централно място. Тези известни открития се намират във всяка математическа теорема от древни времена до скорошните открития на 20-ти век. С всяко ново математическо уравнение идва голям брой нови въпроси и се появяват нови отговори.
Следва антология на някои от математическите теории, които са променили начина, по който виждаме света в ежедневито.

Питагорова теорема
Тази теорема, датираща от 530 г. пр.н.е., вероятно е една от най-популярните математически формули, които съществуват.
Ето я и нея:
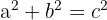
Питагоровата теорема е един от крайъгълните камъни на съвременната математика и значително допринася за развитието на математиката като дисциплина. Дори след много години формулата на тази теорема остава вкоренена в паметта ни.
Теоремата гласи, че в правоъгълен триъгълник квадратът на хипотенузата е равен на сумата от квадратите на другите две страни.
Благодарение на Питагор можем лесно да изчисляваме дължини, ъгли и да определяме дали един триъгълник е правоъгълен или не. Това уравнение е само един от многото математически примери в модерния свят за това как математиката е част от нашето ежедневие, независимо дали го осъзнаваме или не.
Питагоровата теорема продължава да се използва в практически области като строителство, архитектура и дърводелство, между другото.
Универсален закон за гравитацията
Тази сила е право пропорционална на произведението от масите на телата и обратно пропорционална на квадрата на разстоянието между тях.
Например Земята привлича Луната и обратното.
Същият закон се прилага за привличането между ябълка и Земята и привличането между планетите и Слънцето: Универсалният закон за гравитацията.
Този закон и една от най-известните съществуващи математически теории е създаден от Исак Нютон през 17 век.
Намерете своя учител по математика в Superprof!
Формулата е следната:
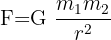
Където:
F: Гравитационна сила (N: Нютони)
M: Маса на първото тяло (обикновено планета, kg)
m: Маса на второто тяло (kg)
R: Разстояние между телата (метри)
G: Гравитационна константа
Гравитационното взаимодействие е универсално. Прилага се за всички видове материя. А гравитацията се проявява само като привличане; не отчита отблъскването на телата.
Теория на относителността
Чистата математика е по свой начин поезията на логическите идеи.
Алберт Айнщайн
Теорията на относителността е една от най-известните математически формули. И въпреки това никой не я разбира напълно.
Теорията на относителността е разработена от Алберт Айнщайн, който помогна за революция в нашето научно разбиране за природата на пространството и времето.
Ограничената теория на относителността въведе идеята, че скоростта на светлината е универсална константа, която не се променя, и че времето не е еднакво за телата, движещи се с различни скорости.
Теорията на относителността е най-известната математическа теория в света, тъй като тя доказа колко важна е математиката в реалния живот и основното въздействие математиката може да има в хода на историята.
Площ на кръг
Кръгът е затворена плоска крива, където всички точки са на еднакво разстояние от центъра. С прости думи, кръгът е затворена линия, като пръстен или гума.
Формулата му е:
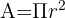
Където
𝐴 е площта на кръга.
След това имаме π (π = 3,1416)
и след това 𝑟, което представлява радиуса на окръжността. Радиусът е разстоянието между центъра на окръжността и всяка точка от нейната граница.
Независимо дали за практически цели, като рисуване на кръгла маса, или във физиката, площта на кръга е от съществено значение.
Благодарение на площта на кръга успяхме да изучаваме вълнови явления, електромагнитни полета, лещи и дори разпределението на светлината в по-голяма дълбочина.

Теория на хаоса
Теорията на хаоса е наука за неочакваното, нелинейното и непредвидимото. Това е една от най-и известните математически теории.
Тази теория се занимава с нелинейни явления, които е практически невъзможно да се предвидят или контролират, като турбуленция, време, фондови пазари, състояния на мозъка и други. Тези явления често се описват с помощта на фрактална математика, която отразява безкрайната сложност на природата.
Теорията на хаоса обхваща например ефекта на пеперудата. Този ефект често се описва по следния начин: пеперуда, която маха с крила в Австралия, може да предизвика ураган в Чили. Може да звучи като фантазия, нали? Теорията на хаоса обаче допуска този ефект да съществува. По-конкретно, пеперудата ефект означава, че малки промени в първоначалните условия могат да доведат до драстични промени в резултатите.
Нашият живот е постоянна демонстрация на този принцип. Тъй като никога не можем да знаем достатъчно подробно всички първоначални условия в една сложна система, не можем да очакваме да предвидим нейния резултат. Това може да е в пряко противоречие с идеята ви за използване на математика покер, тъй като дори малките грешки в измерването на състоянието на системата ще бъдат значително увеличени, правейки прогнозирането безполезно. Това е една от най-интересните математически теории.
Самоличността на Ойлер
Идентичността на Ойлер се дава от следното уравнение:
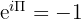
Много математици и експерти смятат това уравнение за едно от най-забележителните, създавани някога.
Това не е само заради неговата елегантност, но и защото обединява пет важни математически константи в една формула:
- e: основата на естествените логаритми
- i: въображаемата единица
- π: 3,1416
- 1 и 0: цели числа
Елегантността на Идентичността на Ойлер се крие в нейната простота.
💡Благодарение на тази простота той оказва значително влияние върху области като инженерство, теория на числата и сложни функции, наред с други.
Идентичността на Ойлер е равенството, където e е числото на Ойлер, основата на естествените логаритми, i е имагинерната единица, която удовлетворява i2 = −1, а π е pi, съотношението на обиколката на кръг към неговия диаметър.
Вторият закон на термодинамиката
Първият закон на топлинната динамика уточнява, че енергията може да се обменя между физически системи във вид на топлина. Вторият закон въвежда друго количество, известно като ентропия.
Това е принцип на промяна и еволюция, тъй като определя в каква посока са възможни потенциални енергийни трансформации. По-просто казано, този закон гласи, че е невъзможно един процес да има като единствен резултат преноса на топлина от по-студено тяло към по-горещо.
Следователно, някои химични трансформации са възможни, докато други никога няма да бъдат. Можете да твърдите със сигурност, например, че ако поставите кубче лед в чаша горещо кафе, кубчето лед ще се разтопи, докато кафето няма да замръзне.
Вторият закон на термодинамиката е физически принцип, който налага ограничение върху посоката на процесите на пренос на топлина между телата.
Намерете своя учител по математика в Superprof!
Въпреки че няколко учени са допринесли за принципите на този закон в миналото, популярността му е достигната през 1873 г. благодарение на Лудвиг Болцмани и Макс Планк. Този закон въвежда концепцията за ентропия, която определя посоката, в която протичат енергийните трансформации.
Уравнението на Шрьодингер
Това уравнение е една от най-известните математически формули. Не, този път не говорим за котката; говорим за друга от брилянтните идеи на Шрьодингер (Нобелова награда за физика).
Уравнението на Шрьодингер е от съществено значение за разбирането как частиците се променят с времето. То ни помага да опишем различните състояния, в които може да се намери една частица.
Освен техническото си значение, това уравнение повдига завладяващ философски въпрос: Материята наистина ли е съставена от конкретни физически състояния, като твърди вещества, течности и газове, или има нещо повече? С други думи, то ни кани да разсъждаваме върху самата природа на материята и как я възприемаме. Този тип математически енигми са много често срещани и това уравнение е врата към отговори, които още предстои бъдат намерени.
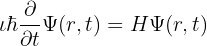
Уравнението на Шрьодингер беше много полезно за напредъка на ядрената енергия, както и за компютърни и лазерни приложения.
Благодарение на това уравнение, едно от най-известните математически уравнения в историята, успяхме да обясним по-добре поведението на атомите и субатомните частици.
Уравнението на Шрьодингер обяснява промените във времето на една частица. Той описва състоянията на частица, от които е възможно да се опише всяко състояние.
Уравнения на Максуел
Четирите уравнения на Максуел формират една от най-важните основи на съвременната физика. Тези уравнения са много важни както за електродинамиката, така и за теорията на относителността.
Уравненията на Максуел са както следва:

Откриването на уравненията на Максуел се счита за върха на класическата физика, тъй като всички уравнения на електромагнетизма могат да бъдат извлечени от тях. Тези уравнения описват взаимодействието между електрическите и магнитните полета и тяхната връзка с електрическите полета и зарядите. Както електричните, така и магнитните полета могат да бъдат представени с помощта на диаграми на полеви линии. Тези уравнения със сигурност повлияват на важността на математиката в съвременния свят, правейки я неразделна част от нашето общество.
Изразени графично, и двете представляват упражняване на сила върху зарядите. С прости думи можем да кажем, че електрическите и магнитните полета са свързани. Те взаимодействат едно с друго и могат да бъдат модифицирани.
Тези известни уравнения са допринесли значително за математиката. Те са позволили да бъдат създадени и усъвършенствани други математически концепции.
Всички тези известни математически уравнения имат нещо общо: те са елегантни, стегнати и помагат да се свърже основната математика с по-прости концепции. Всяко от тези уравнения има обширни и дълбоки приложения в ежедневието и в различни дисциплини, което ги прави толкова ценни. И въпреки че математиката може да е сложна, тя остава завладяваща.
Ако все още ви препоръчваме да разгледате и различни математически ребуси и пъзели.